Introduction
This is an abstract of the LoLA documentation (the full manual is available here).
Please refer to this full documentation for more details on LoLA
The LoLA CTL documentation
LoLA can model check formulae
of the branching time temporal logic CTL as well as an extension of CTL
where path quantifiers can be narrowed to subsets of transitions. We start
with basic CTL formulae for low level net input, proceed with CTL for
high level nets and finish with extended CTL formulae.
CTL is build from atomic propositions which can
be combined via boolean connectives and temporal operators. Thereby, temporal
operators are always combined with a path quantifier.
In LoLA, atomic propositions
always concern the number of tokens on a place. This number can be compared
with a constant number using the binary relations =,#,<>,<=,>=,<,>
where # and <> denote inequality while the meaning
of the remaining operators should be clear. An atomic proposition place
REL number holds in a state s if
the number of tokens on place in state s
relates to number as specified by REL.
As boolean connectives,
the binary operators AND and OR as well as the unary
NOT with their obvious meanings can be used. Parenthesis can
be used to control the execution order of operations.
CTL provides the following
temporal operators: X (next step), F (eventually), G
(globally), and U (until) in combination
with universal (A) and existential
(E) path quantification. In LoLA, these letters are replaced by the following keywords:
| X |
NEXTSTEP |
| F |
EVENTUALLY |
| G |
ALWAYS |
| U |
UNTIL |
| A |
ALLPATH |
| E |
EXPATH |
Since an UNTIL-formula has two subformulae, it is
specified as follows:
ALLPATH [ sub1 UNTIL sub2 ]
In an analysis task file, a CTL formula is announced
by the keyword formulA.
Example of an analysis task file containing
a CTL formula:
formulA ALLPATH EVENTUALLY ( hasright > 3
OR EXPATH NEXTSTEP ALLPATH [ hasleft # 3 UNTIL eating = 0 ] )
For high level nets, a richer language can be used
for CTL formulae. As in the net file, there is an alternative way to specify
instances of high level places using the name dot expression notation.
As the only difference, expression must be enclosed in parenthesis. However,
there are more constructs in HL CTL formulae. First, it is possible to
use variable quantification.
for an arbitrary CTL formula F,
the strings
ALL var : sort : F
and
EXISTS var : sort : F
are CTL formulae, too, where var is a name
of a currently not visible variable, and sort is a sort description
as in the HL net file. A variable that has been introduced this way, may
appear in expressions that specify place instances, such as:
ALL x : phil : hasleft . ( x ) > 3
In HL net formulae, the number a place is compared
with in atomic propositions, can be an arbitrary integer expression, too.
However, unless it is an integer constant, this expression must be enclosed
in parenthesis, too, as in:
ALL x : phil : eating . ( x ) = ( x MOD 2 )
specifying that all philosophers with odd indices
are eating.
As the last HL feature in CTL formulae, arbitrary
boolean expressions, possibly containing quantified variables, can be
used as additional atomic propositions in CTL formulae. These must be
enclosed in brackets, as in
EXPATH EVENTUALLY ALL x : phil : [ x = 3 ] OR
hasright . ( x ) > 0
specifying that all instances of hasright, except
hasright.3, can be marked at the same time.
Before a formula is used in state space generation
or model checking, it
is subject to several transformations. First, all quantifiers are resolved
to large conjunctions or disjunctions. Then, all formulas where the value
does not depend on a state are evaluated. This concerns bracketed boolean
expressions as well as atomic propositions for isolated places (places
where no transition removes or adds tokens). Furthermore, chains of AND
as well as chains of OR are transformed to a single k-ary
AND or OR operation. If, for instance, in the last recent example phil
= [ 1 , 5 ], the formula will internally represented as
EXPATH EVENTUALLY AND(hasright.1 > 0, hasright.2
> 0, hasright.4 > 0,hasright.5 > 0)
which is, in this syntax, not a valid CTL formula
but illustrates LoLA's internal representation. The check for hasright.3
> 0 disappeared since it is ORed to
the true statement 3=3.
Pre-processing constant formulae may influence the shape of temporal operators, or make boolean connectives disappear. The following table lists the possible changes
| Formula |
changes to |
| NOT trUE |
FALSE |
| NOT FALSE |
trUE |
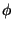 OR trUE OR trUE |
trUE |
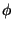 OR FALSE OR FALSE |
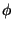 |
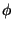 AND trUE AND trUE |
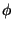 |
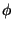 AND FALSE AND FALSE |
FALSE |
| EXPATH NEXTSTEP FALSE |
FALSE |
| EXPATH NEXTSTEP trUE |
trUE |
| EXPATH EVENTUALLY FALSE |
FALSE |
| EXPATH EVENTUALLY trUE |
trUE |
| EXPATH ALWAYS FALSE |
FALSE |
| EXPATH ALWAYS trUE |
trUE |
EXPATH 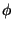 UNTIL FALSE UNTIL FALSE |
FALSE |
EXPATH 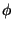 UNTIL trUE UNTIL trUE |
trUE |
EXPATH FALSE UNTIL 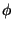 |
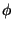 |
EXPATH trUE UNTIL 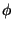 |
EXPATH EVENTUALLY 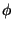 |
Additionally, de Morgan's rules are applied to those
sub-formulae that do not contain temporal operators. Negated comparisons
are replaced by the corresponding comparison (for instance, NOT p
> 3 is replaced by p <= 3. For formulae that contain
temporal operators in sub-formulae, de Morgan's rules are not applied,
so negation symbols are left untouched there.
Let U be
a set of transitions. Then LoLA offers an extension of CTL where
path quantifiers only apply to paths that are built from transitions in U. That is, 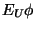 is true if there exists a firing sequence
only using transitions in U where is true if there exists a firing sequence
only using transitions in U where 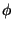 is satisfied. Likewise, is satisfied. Likewise, 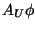 is true if all firing sequences where only
transitions in U occur, satisfy is true if all firing sequences where only
transitions in U occur, satisfy 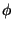 . For more details concerning this CTL extensions,
we refer the reader to [Roc00]. . For more details concerning this CTL extensions,
we refer the reader to [Roc00].
In LoLA, transition sets are specified as boolean
formulas over transitions or transition instances. Thereby a transition
name stands for a singleton set containing the mentioned transition, AND
for intersection, OR for union, and NOT for complement. The specification
of a path restriction is inserted immediately following the path quantifier:
EXPATH t1 OR t2 EVENTUALLY EXPATH NOT t1 AND
NOT t2 EVENTUALLY p > 3
is true iff a state satisfying p
> 3 can be reached from the initial state by a
sequence w1 w2
where w1 consists only
of occurrences of t1 and t2 while neither t1 nor t2 occur in w2.
In the high level case, variable quantification
as well as transition instance specification via the syntax name .
firing mode can be used, as in the example
ALLPATH EXISTS x : [ 1 , 3 ] : tr . [ y1 = x
| y2 = 2 * x ] ALWAYS p = 1
specifying that p will contain one token as long
as only transition instances tr.[y1=1|y2=2], tr.[y1=2|y2=4],
or tr.[y1=3|y2=6] fire.
For considering extended CTL formulae in model checking,
the file userconfig.H must contain a line #define EXTENDEDCTL.
If this option is not set, LoLA accepts path restrictions as input, but
ignores them in verification. Ignoring path restrictions makes LoLA run
a little bit faster.
Roc00
Stephan Roch.
extended Computation Tree Logic.
Workshop Concurrency, Specification & Programming, pages
225-234, 2000.
|









